
সুচিপত্র:
- ধাপ 1: অ্যাডজেসেন্সি ম্যাট্রিক্স তৈরি করুন
- পদক্ষেপ 2: সম্পর্ক তৈরি করুন।
- ধাপ 3: রোগের পরিসংখ্যান যোগ করুন।
- ধাপ 4: র্যান্ডমাইজ করার সম্ভাবনা একটি টিকাযুক্ত এবং অপ্রচলিত ব্যক্তি সংক্রামিত হতে পারে।
- ধাপ 5: প্রাথমিক তথ্য থেকে অসম্পূর্ণ এবং সংক্রামিত ব্যক্তিদের ম্যাট্রিক্স তৈরি করুন।
- ধাপ 6: প্লট প্রাথমিক গ্রাফ।
- ধাপ 7: সংক্রমণের অগ্রগতি অনুকরণ করুন।
- ধাপ 8: মন্টে কার্লো তত্ত্ব ব্যবহার করুন।
- ধাপ 9: একটি ফাংশনে সিমুলেশন দিয়ে ফাইল ('infectionSim.m') তৈরি করুন।
- ধাপ 10: সংক্রামিত এবং টিকা না দেওয়া লোকদের শতকরা হার গণনা করুন।
- ধাপ 11: আপনার ফাংশনে একটি ইনপুট ভেরিয়েবল তৈরি করুন 'infectionSim.m'
- ধাপ 12: ব্যবহারকারীর কাছ থেকে সিমুলেশনের প্রাথমিক শর্ত পেতে একটি মেনু তৈরি করুন।
- ধাপ 13: অপ্রচলিত লোকদের একটি % চয়ন করুন এবং নির্বাচিত শতাংশের জন্য অসম্পূর্ণ এবং সংক্রমিতদের গড় গণনা করুন।
- ধাপ 14: গ্রাফ: 'অসম্পূর্ণ বনাম সংক্রমণের প্রবণতা। নির্দিষ্ট রোগের জন্য টিকা দেওয়া হয়েছে '
- ধাপ 15: চূড়ান্ত পণ্য: সিমুলেশন কেমন দেখাচ্ছে
- লেখক John Day [email protected].
- Public 2024-01-30 08:02.
- সর্বশেষ পরিবর্তিত 2025-01-23 14:36.

প্রকল্পের সংক্ষিপ্ত বিবরণ:
আমাদের প্রকল্প পালের রোগ প্রতিরোধ ক্ষমতা অন্বেষণ করে এবং আমাদের সম্প্রদায়ের সংক্রমণের হার কমাতে মানুষকে টিকা নিতে উৎসাহিত করার আশা করে। আমাদের কর্মসূচী অনুকরণ করে কিভাবে একটি রোগ জনসংখ্যাকে টিকায় এবং টিকা ছাড়ানো হারের বিভিন্ন শতাংশের সাথে সংক্রমিত করে। এটি টিকার জনসংখ্যার বর্ধিত সংখ্যা কীভাবে আক্রান্ত মানুষের সংখ্যা হ্রাস করতে পারে তা দেখিয়ে পালের অনাক্রম্যতা দেখায়।
আমরা গ্রাফ তত্ত্ব ধারণা ব্যবহার করে ম্যাটল্যাবে এটি মডেল করি। গ্রাফ তত্ত্ব বস্তুর মধ্যে সম্পর্কের প্রতিনিধিত্ব করার একটি গাণিতিক উপায়। গ্রাফ তত্ত্বে, গ্রাফের প্রান্ত (বা রেখা) দ্বারা সংযুক্ত শিরোনাম (বা নোড) থাকে। আমাদের প্রকল্পের জন্য, নোডগুলি সংশ্লিষ্ট ব্যক্তি এবং প্রান্তগুলি তাদের সংযোগ। উদাহরণস্বরূপ, যদি দুটি নোড একটি প্রান্তের সাথে সংযুক্ত থাকে তবে এর অর্থ হল তারা "বন্ধু" বা একে অপরের সাথে কোন না কোন ধরনের যোগাযোগ আছে। এই যোগাযোগ রোগ ছড়ানোর একটি উপায়। এই কারণেই আমরা আমাদের ধারণার মডেল করার জন্য গ্রাফ তত্ত্ব ব্যবহার করেছি কারণ আমরা দেখতে চেয়েছিলাম কিভাবে জনসংখ্যার সাথে সংযুক্ত ব্যক্তিদের মধ্যে রোগ ছড়িয়ে পড়ে।
আমাদের প্রকল্পে মন্টে কার্লো পদ্ধতিও জড়িত। মন্টে কার্লো পদ্ধতি হল অ্যালগরিদম যা সংখ্যাসূচক ফলাফল পেতে বারবার এলোমেলো নমুনা তৈরি করে। আমাদের প্রকল্পে, আমরা এই পদ্ধতিটি ব্যবহার করে আমাদের সিমুলেশন চালানোর জন্য কয়েকবার প্রাথমিক অনাক্রম্যতার শতকরা হার পরিবর্তন করে দেখছি যে হারে মানুষ সংক্রমিত হয়।
সমস্ত প্রকল্প কোড নীচে সংযুক্ত করা হয়!
পিসি ক্রেডিট:
গ্রাফ থিওরির সাথে ম্যাটল্যাব লিঙ্ক:
ধাপ 1: অ্যাডজেসেন্সি ম্যাট্রিক্স তৈরি করুন


একটি নতুন স্ক্রিপ্ট তৈরি করুন। আমরা আমাদের 'infectionSim.m' বলে ডাকতে যাচ্ছি।
আমরা একটি পরিবর্তনশীল 'NUMOFPEOPLE' তৈরি করতে যাচ্ছি। আপনি এটিকে যেকোনো পূর্ণসংখ্যার মান নির্ধারণ করতে পারেন। এটি আপনার জনসংখ্যার জনসংখ্যার প্রতিনিধিত্ব করবে।
এখন থেকে, আমরা এটি ধরে নেব
NUMOFPEOPLE = 20;
প্রথমে অনির্দেশিত গ্রাফের জন্য ম্যাটল্যাবের গ্রাফ তত্ত্ব ফাংশন ব্যবহার করে শুরু করুন।
আপনি যদি আরও শিখতে আগ্রহী হন, তাহলে এটি সম্পর্কে আরও গভীরভাবে পড়ার জন্য এখানে একটি লিঙ্ক রয়েছে।
www.mathworks.com/help/matlab/math/directed-and-undirected-graphs.html
একটি সংলগ্ন ম্যাট্রিক্স তৈরি করা হয়েছে।
adjMatrix = শূন্য (NUMOFPEOPLE);
এটি 0s এর একটি বর্গ ম্যাট্রিক্স তৈরি করবে। ম্যাট্রিক্সের প্রতিটি সারি একজন ব্যক্তি। ম্যাট্রিক্সের প্রতিটি কলামই একজন ব্যক্তি বা বন্ধু যার সাথে ব্যক্তিটি সারা দিন দেখা করে।
20 জন মানুষের জন্য adjMatrix দেখতে কেমন তা কল্পনা করতে সাহায্য করার জন্য চিত্র 100 (উপরে) দেখুন।
** এই বিন্দু থেকে আমরা ধরে নেব NUMOFPEOPLE 20 এর সমান। **
আপনি এই সংলগ্ন ম্যাট্রিক্স চক্রান্ত করার চেষ্টা করতে পারেন। এখানে এই ধরনের ম্যাট্রিক্স চক্রান্ত সম্পর্কে আরও কিছু তথ্য রয়েছে।
দ্রষ্টব্য: সংযোজন ম্যাট্রিক্স কিভাবে কাজ করে।
প্রাক্তন:
%সংলগ্ন ম্যাট্রিক্স তৈরি করছে
a = [0, 1, 0, 0, 0; 1, 0, 1, 1, 1; 0, 1, 0, 0, 0; 0, 1, 0, 0, 0; 0, 1, 0, 0, 0] %চক্রান্ত g = গ্রাফ (a); গ্রাফ ফাংশন (গ্রাফ থিওরি) ফিগার (1) ব্যবহার করে %; h = চক্রান্ত (g);
"নোট" এ কোডটি ব্যবহার করে কিভাবে সংলগ্ন ম্যাট্রিক্সে প্রান্ত যুক্ত করতে হয় তা দেখতে চিত্র 1 (উপরে) দেখুন।
পদক্ষেপ 2: সম্পর্ক তৈরি করুন।

এখন যেহেতু মানুষ (শিরোনাম বা নোড) তৈরি করা হয়েছে, আমাদের সম্পর্কের একটি নেটওয়ার্ক (গ্রাফের লাইন বা প্রান্ত) তৈরি করতে হবে। এটি অনুকরণ করবে কিভাবে মানুষ সারা দিন ধরে অন্যদের সাথে যোগাযোগ করে এবং তাদের সাথে দেখা করে।
এটি অনেক উপায়ে করা যেতে পারে। এই কাজটি সম্পন্ন করার একটি উপায় হল প্রতিটি ব্যক্তিকে একটি দিনে একটি র্যান্ডম নম্বর নির্ধারণ করতে হবে যাতে প্রতিটি ব্যক্তি দিনে কতজন মানুষের সাথে যোগাযোগ করবে।
numOfFriendsMatrix = randi ([leastFriendsPersonCanHave, mostFriendsPersonCanHave], 1, NUMOFPEOPLE);
এটি র্যান্ডম পূর্ণসংখ্যার 1 বাই 20 ম্যাট্রিক্স তৈরি করে যা প্রতিটি ব্যক্তির একটি দিনের ইন্টারঅ্যাকশনের সংখ্যা প্রতিনিধিত্ব করে। এই ম্যাট্রিক্সের কলাম প্রতিটি ব্যক্তির সাথে সংশ্লিষ্ট সংখ্যা হবে। উদাহরণস্বরূপ, যদি আমরা ন্যূনতম ফ্রেন্ডসপারসনক্যানহ্যাভ = 2 এবং সর্বাধিক ফ্রেন্ডসপারসনকানহেভ = 5 বরাদ্দ করি, তাহলে আমরা 2 থেকে 5 এর মধ্যে এলোমেলো মান পাব।
Randi () নিয়ে সমস্যা হচ্ছে? টার্মিনালে, টাইপ করুন
রেন্ডিকে সাহায্য করুন
এরপরে, জনসংখ্যার প্রতিটি মানুষ কীভাবে জনসংখ্যার মধ্যে সংযুক্ত/মিথস্ক্রিয়া করে তার একটি এলোমেলো ম্যাট্রিক্স (যাকে "allFriendsmatrix" বলা হয়) তৈরি করি।
tempMatrix = ;
গণনা = 0; allFriendsMatrix = ; k = 1 এর জন্য: NUMOFPEOPLE যখন দৈর্ঘ্য (tempMatrix) ~ = numOfFriendsMatrix (k) count = count +1; temp = Randi ([1, NUMOFPEOPLE]); tempMatrix (count) = temp; দৈর্ঘ্য (tempMatrix) clear = 9 tempMatrix = [tempMatrix, NaN] শেষ করুন end allFriendsMatrix = [allFriendsMatrix; tempMatrix]; tempMatrix = ; গণনা = 0; শেষ
কোডের গভীর ব্যাখ্যা:
প্রথমে আমরা প্রতিটি ব্যক্তির বন্ধু/মিথস্ক্রিয়া তালিকা রাখার জন্য একটি খালি অস্থায়ী ম্যাট্রিক্স তৈরি করি। আমরা গণনাও শুরু করি, যা টেম্পম্যাট্রিক্সে নতুন এলোমেলো সংযোগটি কোথায় আটকে রাখা যায় তার উপর নজর রাখে। লুপগুলির জন্য 20 বার চালানো হয় যাতে জনসংখ্যার প্রতিটি ব্যক্তির জন্য এটি ঘটে। প্রথম যখন লুপ চলবে যতক্ষণ না প্রতিটি ব্যক্তির tempMatrix এলোমেলোভাবে নির্ধারিত মিথস্ক্রিয়া সংখ্যার সমান দৈর্ঘ্য। এই লুপে, জনসংখ্যার ব্যক্তির সাথে সম্পর্কিত একটি এলোমেলো সংখ্যা তৈরি করা হয় এবং tempMatrix এ স্থাপন করা হয়। যেহেতু প্রতিটি tempMatrixes এর দৈর্ঘ্য ভিন্ন, আমাদের কিছু NaN মান তৈরি করতে হবে যাতে আমরা এই সমস্ত tempMaticles কে এক ম্যাট্রিক্সে ('allFriendsMatrix') একত্রিত করতে পারি। দ্বিতীয় সময় লুপ প্রতিটি tempMatrix- এ NaN যোগ করে এই সমস্যার সমাধান করে। যখন লুপটি 9 বার চালানোর জন্য সেট করা হয়েছিল কারণ এটি 5 এর চেয়ে বড় সংখ্যা, যা একজন ব্যক্তির বন্ধুদের উপরের সীমা নির্ধারণ করা যেতে পারে। '9' মানটি পরিবর্তনশীল এবং পরিবর্তন করা যেতে পারে যখন 'mostFriendsPersonCanHave' 9. এর চেয়ে বড় হয়। তারপর এটি tempMatrix সাফ করে এবং পরবর্তী ব্যক্তির জন্য গণনা করে।
আউটপুট
আউটপুটটি লুপের মাধ্যমে প্রথম রান করার জন্য (শেষ তিনটি লাইনের আগে) দেখতে কেমন হওয়া উচিত।
tempMatrix = 16 8 17 16 13 NaN NaN NaN NaN
allFriendsMatrix =
16 8 17 16 13 NaN NaN NaN NaN 8 8 2 7 11 NaN NaN NaN NaN 10 13 NaN NaN NaN NaN NaN NaN 11 17 2 NaN NaN NaN NaN NaN NaN 10 12 NaN NaN NaN NaN NaN NaN 4 13 2 12 NaN NaN NaN NaN NaN 17 10 9 3 1 NaN NaN NaN NaN 16 16 6 NaN NaN NaN NaN NaN NaN 3 8 17 17 14 NaN NaN NaN NaN 20 19 3 NaN NaN NaN NaN NaN 13 10 NaN NaN NaN NaN NaN 2N 18 10 16 NaN NaN NaN NaN NaN 2 6 14 3 13 NaN NaN NaN NaN 8 16 14 8 NaN NaN NaN NaN NaN 7 7 NaN NaN NaN NaN NaN NaN NaN NaN 19 10 9 NaN NaN NaN NaN NaN 10NN 19N 9N NaN NaN NaN 5 18 NaN NaN NaN NaN NaN NaN NaN 1 7 NaN NaN NaN NaN NaN NaN NaN NaN 16 7 13 10 1 NaN NaN NaN NaN
পরবর্তী, এই সম্পর্কগুলিকে adjMatrix- এ যুক্ত করুন।
eachRow = 1: NUMOFPEOPLE এর জন্য
eachCol = 1: 9 এর জন্য যদি isnan (allFriendsMatrix (eachRow, eachCol)) == 0 adjMatrix (eachRow, allFriendsMatrix (eachRow, eachCol)) = 1; adjMatrix (allFriendsMatrix (eachRow, eachCol), eachRow) = 1; শেষ শেষ শেষ
কোড ব্যাখ্যা
লুপের জন্য এই ডাবলটি 'allFriendsMatrix' এর প্রতিটি সারি এবং কলামের মধ্য দিয়ে যায়। If স্টেটমেন্টটি সমস্ত মানগুলির জন্য চালানো হবে যা 'NaN' নয়। মূলত এটি গ্রাফের প্রান্ত বা রেখা তৈরি করবে। সুতরাং এই প্রথম লাইনটি ব্যক্তি 1 থেকে ব্যক্তি 16 এবং ব্যক্তি 16 থেকে ব্যক্তি 1 হবে। কারণ এটি অনির্দেশিত, উভয়কেই 1 পরিবর্তন করতে হবে! আমরা কেবল 1 থেকে 16 প্রান্ত থাকতে পারি না এবং 16 থেকে 1 না। ম্যাটল্যাবে এটি সঠিকভাবে চলার জন্য তাদের অবশ্যই প্রতিসম হতে হবে।
আমাদের অনুকরণে, আমরা প্রতিষ্ঠিত করেছি যে লোকেরা নিজেদের সাথে যোগাযোগ করতে পারে না। যখন আমরা মানগুলিকে এলোমেলো করে দেই, তখন আমাদের আশেপাশের ম্যাট্রিক্সের এই ত্রুটিগুলি হওয়ার সম্ভাবনা থাকে।
আসুন নিম্নলিখিত কোড দিয়ে এটি ঠিক করি:
প্রত্যেকের জন্য = 1: NUMOFPEOPLE
adjMatrix (প্রতিটি, প্রতিটি) = 0; শেষ
কোড ব্যাখ্যা
লুপের জন্য এটি নিশ্চিত করে যে ব্যক্তি 1 ব্যক্তি 1 এর সাথে সংযুক্ত নয়, ব্যক্তি 2 ব্যক্তি 2 এর সাথে সংযুক্ত নয়, ইত্যাদি সবগুলিকে 0 করে। উপরের বাম থেকে নিচের ডানদিকে ম্যাট্রিক্স সব 0।
আউটপুট
এই বর্তমান সিমুলেশনের জন্য এটি চূড়ান্ত adjMatrix। এটি গ্রাফের সমস্ত লাইনের জন্য হিসাব করে (চিত্র 2)।
adjMatrix =
0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 1 1 0 1 1 0 0 0 1 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 1 0 1 1 0 0 0 0 0 1 0 1 0 1 0 0 0 1 1 0 0 0 1 1 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 1 0 1 0 1 0 0 0 0 1 1 1 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 0
'AdjMatrix' এর গ্রাফ দেখতে চিত্র 2 দেখুন।
ধাপ 3: রোগের পরিসংখ্যান যোগ করুন।
এখন যেহেতু আপনার প্রোগ্রাম এলোমেলো মানুষের একটি সেট দিয়ে একটি গ্রাফ তৈরি করতে পারে এবং এলোমেলো সম্পর্ক তৈরি করতে পারে, জনসংখ্যার মধ্যে এই মিথস্ক্রিয়াগুলি কীভাবে সংক্রমণ বৃদ্ধি বা হ্রাস করতে পারে তা দেখতে আমাদের রোগের তথ্য বা পরিসংখ্যান ইনপুট করতে হবে।
এই ভেরিয়েবল তৈরি করুন:
unvacc %টাইপ: ডাবল; টিকা ছাড়ানো লোকদের অসুস্থ না হওয়ার শতকরা সম্ভাবনা
ভ্যাকস %টাইপ: ডাবল; টিকা দেওয়া মানুষের অসুস্থতা না পাওয়ার শতকরা সম্ভাবনা unvacc_perc %টাইপ: দ্বিগুণ; শতাংশ জনসংখ্যা টিকা ছাড়ানো init_infect %type: int; শতাংশ জনসংখ্যার টিকা দেওয়া হয়েছে
পরবর্তী আমাদের কিছু গণনা করতে হবে।
আমরা একটি 'ইনফেকশনম্যাট' তৈরি করতে যাচ্ছি যা 3*NUMOFPEOPLE ম্যাট্রিক্স।
vacc_perc = 1-unvacc_perc;
সংক্রমণ ম্যাট = ন্যান (3, NUMOFPEOPLE); সংখ্যা = বৃত্তাকার (vacc_perc * NUMOFPEOPLE); সংক্রমণ ম্যাট (1, 1: সংখ্যা) = টিকা; সংক্রমণ ম্যাট (1, সংখ্যা+1: শেষ) = unvacc; সংক্রমণ ম্যাট (2, 1: শেষ) = 0; সংক্রমণ ম্যাট (2, 1: init_infect) = 1;
কোড ব্যাখ্যা
লাইন 1: জনসংখ্যার শতাংশ অসংক্রামিত গণনা করা হয়েছে
লাইন 2: 3*N সংখ্যক মানুষের ম্যাট্রিক্স তৈরি করুন
লাইন 3: টিকা দেওয়া শতাংশ থেকে টিকা দেওয়া মানুষের সংখ্যা খুঁজে বের করুন
লাইন 4: টিকা দেওয়া লোকদের জন্য, তাদের টিকা নেওয়ার সাথে সম্পর্কিত একটি অনাক্রম্যতা দিন। এই মানটি রোগ সম্পর্কে গবেষণা থেকে নির্ধারিত হয়।
লাইন 5: বাকি জনসংখ্যার জন্য (টিকা ছাড়ানো ব্যক্তি), তাদের শতকরা অনাক্রম্যতা দিন। এই মানটি রোগ সম্পর্কে গবেষণা থেকে নির্ধারিত হয়।
লাইন 6: প্রাথমিকভাবে সমস্ত মানুষকে সংক্রমিত না করার জন্য সেট করুন।
লাইন 7: প্রাথমিকভাবে সংক্রামিত মানুষের সংখ্যার জন্য, সেই অনুযায়ী প্রথম দম্পতির কলামগুলি পূরণ করুন।
এখন যেহেতু আমরা রোগ সিমুলেশনের জন্য সমস্ত প্যারামিটার সেট করেছি, আমরা ব্যক্তি (টিকা এবং অপ্রকাশিত) উভয়ই সংক্রামিত হওয়ার সম্ভাবনাকে এলোমেলো করতে যাচ্ছি। এই 'ইনফেকশনম্যাট' -এর তৃতীয় সারির প্রতিটি ব্যক্তিকে 0 থেকে 1 এর মধ্যে এলোমেলো মান নির্ধারণ করে পরবর্তী ধাপে এটি করা হয়।
ধাপ 4: র্যান্ডমাইজ করার সম্ভাবনা একটি টিকাযুক্ত এবং অপ্রচলিত ব্যক্তি সংক্রামিত হতে পারে।
এরপরে, প্রতিটি ব্যক্তিকে একটি এলোমেলো নম্বর বরাদ্দ করুন, এটি পরে সংক্রমিত হবে কিনা তা নির্ধারণ করতে ব্যবহার করা হবে।
w = 1 এর জন্য: দৈর্ঘ্য (সংক্রমণ ম্যাট)
সংক্রমণ ম্যাট (3, w) = র্যান্ড; শেষ
কোড ব্যাখ্যা
লুপের জন্য এটি শেষ ধাপে তৈরি 'ইনফেকশনম্যাট' এর তৃতীয় সারির সাথে সম্পর্কিত। 'র্যান্ড' সারি 3 এর প্রতিটি সূচকে 0 এবং 1 এর মধ্যে একটি মান নির্ধারণ করে।
আউটপুট
সংক্রমণ ম্যাট এখন সম্পূর্ণ! এটি এমন একটি জনসংখ্যার সাথে ছিল যেখানে 100% টিকা দেওয়া হয়েছিল এবং 1 জন ব্যক্তি প্রাথমিকভাবে সংক্রামিত হয়েছিল।
সংক্রমণ ম্যাট =
কলাম 1 থেকে 12 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 1.0000 0 0 0 0 0 0 0 0 0 0 0 0 0.0869 0.5489 0.3177 0.9927 0.7236 0.5721 0.7172 0.9766 0.4270 0.9175 0.0000 0.270 0.7500 0.7500 0 0 0 0 0 0 0 0 0.0480 0.3593 0.2958 0.6291 0.1362 0.3740 0.8648 0.2503
সারি 1: রোগ না পাওয়ার শতকরা সম্ভাবনা
সারি 2: সংক্রমিত বা সংক্রমিত নয় (বুলিয়ান মান)
সারি 3: সংক্রামিত নয় এমন ব্যক্তি সংক্রামিত ব্যক্তির সাথে দেখা করলে সংক্রমিত হয় কিনা তা পরীক্ষা করার জন্য ব্যবহৃত নম্বর। যদি অসংক্রমিত ব্যক্তি সংক্রামিত ব্যক্তির সাথে দেখা করে, এই সংখ্যাটি সারি 1 (একই কলামের) সংখ্যার চেয়ে বেশি, তাহলে তারা সংক্রমিত। আমরা ধাপ 7 এ এই কার্যকারিতাটি কোড করব।
ধাপ 5: প্রাথমিক তথ্য থেকে অসম্পূর্ণ এবং সংক্রামিত ব্যক্তিদের ম্যাট্রিক্স তৈরি করুন।
"MatrixUnvacc" এবং "matrixInfected" নামে 2 টি ম্যাট্রিক্স তৈরি করুন যা সমস্ত সংক্রামিত মানুষকে সংক্রমণ ম্যাট থেকে সংরক্ষণ করে। এটি ব্যবহার করা হবে যাতে আমরা সংক্রামিত, টিকা না দেওয়া বা টিকা দেওয়া ব্যক্তিদের গ্রাফকে রঙ-কোড করতে পারি, যাতে টিকা না দেওয়া বনাম টিকা দেওয়া ব্যক্তিদের প্রভাবকে কল্পনা করতে সাহায্য করে।
প্রতিটি পরিষ্কার করুন
matrixInfected = ; matrixUnvacc = ; h = 1: দৈর্ঘ্য (ইনফেকশন ম্যাট) যদি ইনফেকশনম্যাট (1, জ) == আনভ্যাক ম্যাট্রিক্সউনভ্যাক = [ম্যাট্রিক্সউনভ্যাক, এইচ]; ব্যক্তির জন্য শেষ শেষ = 1: NUMOFPEOPLE যদি সংক্রমণ ম্যাট (2, ব্যক্তি) == 1 matrixInfected = [matrixInfected, person]; শেষ শেষ
কোড ব্যাখ্যা
অসম্পূর্ণ এবং সংক্রামিত মানুষের সংখ্যা যথাক্রমে সংরক্ষণ করার জন্য দুটি খালি ম্যাট্রিক্স তৈরি করুন। উভয় লুপের জন্য 20 বার চালানো হয় এবং যদি বিবৃতিটি সন্তুষ্ট হয়, তাহলে সংখ্যাটি সঠিক ম্যাট্রিক্সে যোগ করা হয়।
আউটপুট
matrixUnvacc =
matrixInfected =
[1]
ধাপ 6: প্লট প্রাথমিক গ্রাফ।

পরবর্তী আমরা সংলগ্ন ম্যাট্রিক্স চক্রান্ত করতে যাচ্ছি।
g = গ্রাফ (adjMatrix);
চিত্র (1) p = চক্রান্ত (g, 'NodeColor', 'b', 'MarkerSize', 7); হাইলাইট (p, matrixUnvacc, 'NodeColor', 'g') হাইলাইট (p, matrixInfected, 'NodeColor', 'r') title_unvacc = unvacc_perc*100; শিরোনাম (['অসম্পূর্ণ মানুষের শতাংশ:', num2str (title_unvacc), '%']); বিরতি (গতি)
কোড ব্যাখ্যা
ম্যাটল্যাবে গ্রাফ তত্ত্ব ফাংশন তৈরি করেছে। যখন আমরা গ্রাফ () ফাংশনটি ব্যবহার করি, আমরা 'adjMatrix' কে একটি প্রকৃত অনির্দেশিত গ্রাফে অনুবাদ করতে সক্ষম হই। আমাদের তখন প্লট () ফাংশন ব্যবহার করে একটি প্লট তৈরি করতে হবে যা আসলে দেখতে কেমন। আমরা এই প্লট () কে একটি ভেরিয়েবলে সেট করেছি যাতে আমরা সিমুলেশন জুড়ে প্লটের রঙগুলি আরও সহজে ম্যানিপুলেট এবং পরিবর্তন করতে পারি। সমস্ত মানুষ (বা নোড) প্রাথমিকভাবে 'নীল' রঙে সেট করা আছে। এর পরে, সমস্ত অপ্রচলিত মানুষ 'সবুজ' রঙে সেট করা হয়। সংক্রামিত ব্যক্তিদের তারপর 'লাল' রঙের জন্য সেট করা হয়। শিরোনামটি পরীক্ষা না করা লোকদের নির্দিষ্ট শতাংশ মান অনুযায়ী সেট করা হয়। বিরতি () ফাংশন সাময়িকভাবে ম্যাটল্যাব এক্সিকিউশন বন্ধ করে দেয়। আমরা ভেরিয়েবল স্পিডের মধ্য দিয়ে যাই যা ছড়িয়ে পড়ে যা সেকেন্ডে গণনা করা হয়।
একটি এলোমেলো রঙের কোডেড গ্রাফ দেখতে ছবি (উপরে) দেখুন।
ম্যাটল্যাবে হাইলাইট () ফাংশন সম্পর্কে আরও জানুন।
ধাপ 7: সংক্রমণের অগ্রগতি অনুকরণ করুন।
পরবর্তীতে আমাদের বোঝা দরকার যে ইন্টারঅ্যাকশনের পরে কে সংক্রমিত হয় (অ্যাডজ ম্যাট্রিক্সে রেকর্ড করা আছে) এবং কেউ সংক্রমিত হলে গ্রাফ আপডেট করে।
একদিনে মানুষের সাথে কথোপকথনের পর কোন মানুষ সংক্রমিত তা নির্ধারণ করতে adjMatrix ব্যবহার করুন।
eachRow = 1: length (adjMatrix) এর জন্য
যদি সংক্রমণ ম্যাট (2, eachRow) == 1 forCol = 1: দৈর্ঘ্য (adjMatrix) যদি adjMatrix (eachRow, eachCol) == 1 % eachRow = ব্যক্তি % eachCol = তার বন্ধু % প্রত্যেক ব্যক্তির বন্ধু এবং দেখুন তারা সংক্রামিত হয় কিনা । যদি সংক্রমণ ম্যাট (3, eachCol)> সংক্রমণ ম্যাট (1, eachCol) সংক্রমণ ম্যাট (2, eachCol) = 1; হাইলাইট (p, eachCol, 'NodeColor', 'r') pause (speed) end end end end end
প্রতিটি ব্যক্তির মাধ্যমে লুপ লুপ। এটি পরীক্ষা করে যে যদি ব্যক্তিটি সংক্রামিত হয়, এটি তাদের সাথে যোগাযোগ করা প্রতিটি ব্যক্তি/বন্ধুকে পরীক্ষা করবে এবং পরীক্ষা করবে যে বন্ধুর রোগ প্রতিরোধ ক্ষমতা স্তরটি রোগের শক্তির চেয়ে বেশি ছিল কিনা। এখানেই আমরা আগে তৈরি করা 'ইনফেকশনম্যাট' খেলার মধ্যে আসে। বন্ধুর প্রতিটি কলামের ১ ম এবং row য় সারি তুলনা করা হয় এবং যদি row য় সারি বড় হয়, তাহলে এর মানে হল যে বন্ধুর রোগ প্রতিরোধের জন্য যথেষ্ট উচ্চ রোগ প্রতিরোধ ক্ষমতা ছিল না এবং শেষ পর্যন্ত সংক্রামিত হয়। আমরা সংক্রামিত হলে হাইলাইট () ব্যবহার করে লাল রঙে পরিবর্তন করি।
এখন সিমুলেশন জন্য আপনার কোড কাজ করা উচিত! এবং জনসংখ্যার যেকোনো আকারের জন্য, শুধু NUMOFPEOPLE পরিবর্তন করুন!
ধাপ 8: মন্টে কার্লো তত্ত্ব ব্যবহার করুন।
এটিকে আরও এক ধাপ এগিয়ে নিতে এবং আমাদের সিমুলেটর ('ইনফেকশনসিম.এম') থেকে ডেটা বের করতে, আমরা সংক্রামিত অসংক্রামিত মানুষ এবং সংক্রামিত টিকা দেওয়া লোকের শতাংশের প্রবণতা গণনা এবং গ্রাফ করতে চেয়েছিলাম। আমরা অনুমান করি যে সংক্রামিত টিকা নেওয়া লোকের শতাংশ সংক্রামিত টিকা ছাড়ানো মানুষের শতকরা তুলনায় অনেক কম হওয়া উচিত।
ধাপ 9: একটি ফাংশনে সিমুলেশন দিয়ে ফাইল ('infectionSim.m') তৈরি করুন।
মন্টে কার্লো চালানোর জন্য, আমরা সিমুলেশনটি একাধিকবার চালাতে চাই এবং তথ্য সংগ্রহ করতে চাই যাতে আমরা সংক্রামিত মানুষের শতাংশের গ্রাফ করতে এটি ব্যবহার করতে পারি।
ফাংশন এই মত সেট আপ করা যেতে পারে:
ফাংশন আউটপুট = সংক্রমণ সিম (unvacc, ভ্যাকস, NUMOFPEOPLE, unvacc_perc, init_infect, speed)
আপনার সিমুলেশনের ভেরিয়েবলগুলি মন্তব্য করুন এখন থেকে আপনি এইগুলিকে প্রধান ফাইলের মধ্য দিয়ে যাচ্ছেন (আমরা এটি ধাপ 12 এ লিখতে শুরু করব):
unvacc, ভ্যাকস, NUMOFPEOPLE, unvacc_perc, init_infect
নতুন পরিবর্তনশীল
গতি
প্রধান ফাইলে (Monte_Carlo.m) বরাদ্দ করা হবে।
দ্রষ্টব্য: ফাংশনটি শেষ করতে ফাংশন ফাইলের নীচে শেষটি ভুলে যাবেন না!
ধাপ 10: সংক্রামিত এবং টিকা না দেওয়া লোকদের শতকরা হার গণনা করুন।
এটি সংক্রামিত অসুখী মানুষের শতকরা হিসাব করে। এই কোডটি 'infectionSim.m' ফাইলের নীচে যায়।
number_of_unvacc = 0;
number_of_infec_unvacc = 0; %x = 1 এর জন্য সংক্রামিত অসম্পূর্ণ মানুষের শতাংশ গণনা করে: দৈর্ঘ্য (ইনফেকশন ম্যাট) যদি সংক্রমণ ম্যাট (1, x) == unvacc number_of_unvacc = number_of_unvacc+1; শেষ হলে সংক্রমণ ম্যাট (1, x) == unvacc & infectionMat (2, x) == 1 number_of_infec_unvacc = number_of_infec_unvacc +1; শেষ শেষ শতাংশ_অফ_উনভ্যাক_এন্ড_ইনফেক = (সংখ্যা_অফ_ইনফেক_উনভ্যাক / নম্বর_অফ_উনভ্যাক)*100;
কোড ব্যাখ্যা
লুপে, এটি NUMOFPEOPLE বার লুপ করবে। প্রতিবার সংক্রমণের সংখ্যা ম্যাট আনভ্যাক সংখ্যার সাথে মিলে যায় (অর্থাৎ 0.95 == 0.95), তারপর অসংক্রামিত মানুষের সংখ্যা 1 দ্বারা বৃদ্ধি পাবে। সংক্রমিত এবং টিকা না দেওয়া রোগীর সংখ্যা ১. বৃদ্ধি পায় তারপর এই থেকে শতাংশ গণনা করা হয়।
চ্যালেঞ্জ:
সংক্রামিত ব্যক্তিদের টিকা দেওয়ার শতাংশ গণনা করার চেষ্টা করুন! (ইঙ্গিত: এটি এই উপরের কোডের অনুরূপ, তবে কিছু ভেরিয়েবল পরিবর্তন করা হয়েছে এবং নামগুলি সামঞ্জস্য করা হয়েছে।)
পরবর্তী মোট জনসংখ্যার উপর ভিত্তি করে সংক্রমিত মানুষের শতাংশ গণনা করা হয়:
pre_per_infect = cumsum (ইনফেকশন ম্যাট (2,:));
per_infect = (pre_per_infect (1, NUMOFPEOPLE)/NUMOFPEOPLE)*100;
কোড ব্যাখ্যা
সংক্রামক ম্যাটের দ্বিতীয় সারি ব্যবহার করে সংখ্যার যোগফল গণনা করা হয়, যা ব্যক্তি সংক্রমিত কিনা তা নির্ভর করে 1s এবং 0s সঞ্চয় করে।যেহেতু cumsum () ফাংশনটি একটি ম্যাট্রিক্স ফিরিয়ে দেয়, তাই আমরা ম্যাট্রিক্স ('pre_per_infect (1, NUMOFPEOPLE)') এর শেষ মানটি গ্রহণ করি, যা 'infectionMat (2,:)' থেকে সমস্ত মানগুলির প্রকৃত যোগফল হওয়া উচিত। যোগফলকে NUMOFPEOPLE দ্বারা ভাগ করে এবং 100 দ্বারা গুণ করলে আমরা মোট জনসংখ্যার সংক্রমণের চূড়ান্ত শতাংশ পেতে পারি।
ধাপ 11: আপনার ফাংশনে একটি ইনপুট ভেরিয়েবল তৈরি করুন 'infectionSim.m'
আউটপুট = [per_infect, percent_of_unvacc_and_infec, percent_of_vacc_and_infec];
কোড ব্যাখ্যা
এই তথ্যটি আউটপুটে সংরক্ষণ করুন, যা ফাংশনটি ডেকে এবং চলার পরে প্রধান (Monte_Carlo.m) এ ফেরত পাঠানো হবে। এই ডেটা ব্যবহার করা হয় যারা টিকা এবং অপ্রকাশিত রোগীদের শতকরা সংখ্যার পয়েন্ট গ্রাফ করতে।
আপনার 'infectionSim.m' ফাংশনটি এখনই করা উচিত! যাইহোক, এটি চলবে না কারণ আমাদের এখনও মূল লিখতে হবে!
ধাপ 12: ব্যবহারকারীর কাছ থেকে সিমুলেশনের প্রাথমিক শর্ত পেতে একটি মেনু তৈরি করুন।
মনে রাখবেন কিভাবে আমরা পরিবর্তনশীল বলেছি
গতি
তৈরি করা হবে এবং প্রধান ফাংশন মাধ্যমে পাস? ফাংশনে পাস করার জন্য আমাদের মানগুলি পেতে হবে। নোট, ফাংশন কল করার সময় মানগুলির ক্রমটি গুরুত্বপূর্ণ!
টার্মিনালে কিছু উত্তর টাইপ করতে ব্যবহারকারীকে জিজ্ঞাসা করে শুরু করুন।
> একটি রোগ বাছুন। মনে রাখবেন এটি কেস সংবেদনশীল >> পার্টুসিস >> ফ্লু >> হাম >> রোগ চয়ন: ফ্লু >> জনসংখ্যার আকার বাছুন। >> 20 >> 200 >> জনসংখ্যা নির্বাচিত: 20 >> সিমুলেশনের গতি বাছুন। >> দ্রুত >> ধীর >> গতি নির্বাচিত: দ্রুত
নীচের এই কোডটি ব্যবহারকারীকে জিজ্ঞাসা করে যে তারা কোন রোগটি দেখতে চায়।
ডিসপ ('একটি রোগ বাছুন। লক্ষ্য করুন এটি কেস সংবেদনশীল')
fprintf ('Pertussis F nFlu / n Measles / n') রোগ = ইনপুট ('রোগ নির্বাচিত:', 's'); যদি অসম (রোগ, 'Pertussis') ভ্যাকস =.85; %15 %অসুখ পাওয়ার সম্ভাবনা unvacc =.20; %80 %রোগ পাওয়ার সম্ভাবনা অন্যথায় যদি সমান (রোগ, 'ফ্লু') টিকা =.75; %25 %অসুখ পাওয়ার সম্ভাবনা unvacc =.31; %Percent %রোগ হওয়ার সম্ভাবনা যদি অন্যরকম হয় (অসুখ, 'হাম') টিকা =.97; %3 %অসুখ পাওয়ার সম্ভাবনা unvacc =.10; রোগ শেষ হওয়ার সম্ভাবনা 90 %
কোড ব্যাখ্যা:
ডিসপ () ফাংশন স্ক্রিনে স্টেটমেন্ট প্রিন্ট করে এবং এটি বিভিন্ন অপশন প্রিন্ট করে। সেই অনুযায়ী রোগ নির্ধারিত হবে। এই সংস্করণটি বর্তমানে অবৈধ ইনপুটের জন্য অ্যাকাউন্ট করে না। অবৈধ ইনপুট একটি ত্রুটি উৎপন্ন করবে এবং প্রোগ্রামটি সম্পূর্ণভাবে বন্ধ করে দেবে। প্রতিটি রোগের সাথে ভ্যাকসিন এবং আনভ্যাক মূল্য রয়েছে। এই মানগুলি এলোমেলো নয়। রোগ সম্পর্কে পরিসংখ্যান গবেষণা করে আমরা এই মানগুলি পেয়েছি।
এরপরে, আমাদের ব্যবহারকারীকে জিজ্ঞাসা করা উচিত যে তারা তাদের নির্বাচিত রোগের জন্য বড় বা ছোট জনসংখ্যার আকার পরীক্ষা করতে চায় কিনা।
ডিসপ ('জনসংখ্যার আকার বাছুন।')
fprintf ('20 / n200 / n ') গতি = ইনপুট (' জনসংখ্যা নির্বাচিত: ',' s '); যদি সমান (গতি, '20') জনসংখ্যার আকার = 20; অন্য যদি সমান (গতি, '200') জনসংখ্যার আকার = 200; শেষ
কোড ব্যাখ্যা
এটি ব্যবহারকারীর কাছে একটি বিবৃতি প্রিন্ট করে এবং ব্যবহারকারীকে কোন আকারের জনসংখ্যা পরীক্ষা করতে চায় তা প্রবেশ করতে বলে। এই সংস্করণটি বর্তমানে অবৈধ ইনপুটের জন্য অ্যাকাউন্ট করে না। অবৈধ ইনপুট একটি ত্রুটি উৎপন্ন করবে এবং প্রোগ্রামটি সম্পূর্ণভাবে বন্ধ করে দেবে। 20 টি বাছাই করা হয়েছিল কারণ এটি একটি ছোট নমুনার আকার যা এখনও একটি ছোট জনসংখ্যা জুড়ে কীভাবে সংক্রমণ ছড়িয়ে পড়ে সে সম্পর্কে একটি ভাল ধারণা দেয়। 200 জনকে বৃহত্তর বিকল্প হিসাবে বেছে নেওয়া হয়েছিল কারণ গ্রাফে 200 পয়েন্টের প্লট করা ছিল বিন্দু মাত্র কোন পয়েন্ট ছিল না যাতে সবকিছু সহজেই দেখা যায় এবং একে অপরের থেকে আলাদা করা যায়।
পরবর্তী, আমাদের সিমুলেশনের গতি খুঁজে বের করতে হবে।
ডিসপ ('সিমুলেশনের গতি বাছুন।')
fprintf ('দ্রুত / n ধীর / n') গতি = ইনপুট ('গতি নির্বাচিত:', 's'); যদি সমান (গতি, 'দ্রুত') sim_speed = 0; elseif isequal (speed, 'slow') sim_speed = 0.25; শেষ
কোড ব্যাখ্যা
এই প্রক্রিয়াটি রোগের ধরন এবং জনসংখ্যার আকার পাওয়ার মতোই ছিল। দ্রুত জন্য, কোন বিরতি থাকবে। এবং ধীর গতিতে, সিমুলেশন চালানোর সময় লুপের জন্য 0.25 সেকেন্ড ল্যাগ থাকবে।
দারুণ! এখন আমাদের ব্যবহারকারীর সমস্ত ইনপুট আমাদের প্রয়োজন! আসুন অপ্রচলিত মানুষের বিভিন্ন শতাংশের জন্য তথ্য সংগ্রহের দিকে এগিয়ে যাই।
ধাপ 13: অপ্রচলিত লোকদের একটি % চয়ন করুন এবং নির্বাচিত শতাংশের জন্য অসম্পূর্ণ এবং সংক্রমিতদের গড় গণনা করুন।
এই কোডটি 0% টিকা ছাড়ানো মানুষের জন্য।
% ------- % 0 অপ্রচলিত ------------
per_infect_av_0 = ; শতাংশ_অনভ্যাক_এন্ড_ইনফেক_এভ_0 = ; i = 1:20 out = infectionSim (unvacc, vacc, Population_size, 0, 1, sim_speed); per_infect_av_0 = [per_infect_av_0, out (1, 1)]; শতকরা_একটি শেষ গড়_ সংক্রমিত_0 = গড় (প্রতি_ইনফেক্ট_এভ_0); গড়_ unvacc_and_infected_0 = গড় (শতাংশ_ এর_অনভ্যাক_এন্ড_ইনফেক_এভ_0);
কোড ব্যাখ্যা:
লুপের জন্য 20 বার চালানো হয়। ইনফেকশন সিম () ফাংশন থেকে আউটপুট আউট স্টোর করা হয়। প্রতিবার লুপ চলার পর, মোট জনসংখ্যার সংক্রমণের শতাংশ ম্যাট্রিক্সে যোগ করা হয়, 'per_infect_av_0'। অতিরিক্তভাবে, প্রতিবার টিকা ছাড়ানো এবং সংক্রমণের শতাংশও 'শতাংশ_অফ_উনভ্যাক_এন্ড_ইনফেক_এভ_0' ম্যাট্রিক্সে যোগ করা হয়। শেষ দুটি লাইনে, এই দুটি, উপরে উল্লিখিত ম্যাট্রিক্সগুলি তারপর গড় এবং ভেরিয়েবলে সংরক্ষণ করা হয়। সংক্ষেপে বলতে গেলে, প্রতিটি সিমুলেশন, গড়, এবং গ্রাফেডের জন্য শতাংশ সংরক্ষণ করা হয়। মন্টে কার্লো একটি সিমুলেশন চালানোর গড় ফলাফল এবং ফলাফল দেখানোর জন্য ব্যবহৃত হয়। আমাদের পরীক্ষামূলক উদ্দেশ্যে, আমরা 20 বার সিমুলেশন চালানো এবং সেই মানগুলির গড় গড়তে পছন্দ করি।
চ্যালেঞ্জ:
আপনি পরীক্ষা করতে চান এমন সমস্ত শতাংশের জন্য পুনরাবৃত্তি করুন! শতকরা সংখ্যা অনুযায়ী পরিবর্তনশীল নাম পরিবর্তন করে এটি করা যেতে পারে। আমরা 0%, 5%, 10%, 20%, 30%এবং 50%পরীক্ষা করেছি।
ইঙ্গিত:
একমাত্র কোড যা প্রকৃত কোডে পরিবর্তন করা আবশ্যক
out = infectionSim (unvacc, vacc, Population_size, 0, 1, sim_speed);
দশমিক আকারে শূন্যকে শতাংশে পরিবর্তন করুন। উদাহরণস্বরূপ, 5% অপ্রচলিত সিমুলেশনের জন্য, 0 কে 0.5 দিয়ে প্রতিস্থাপন করা উচিত।
ধাপ 14: গ্রাফ: 'অসম্পূর্ণ বনাম সংক্রমণের প্রবণতা। নির্দিষ্ট রোগের জন্য টিকা দেওয়া হয়েছে '
অসম্পূর্ণ ব্যক্তি বনাম অপ্রকাশিত ব্যক্তিদের মধ্যে সংক্রমণের প্রবণতার একটি গ্রাফ তৈরি করার জন্য এটি কোড।
graph_mat_y = [average_infected_0, average_infected_5, average_infected_10, average_infected_20, average_infected_30, average_infected_50];
graph_mat_x = [0, 5, 10, 20, 30, 50]; opeাল = (গড়_ সংক্রমিত_5-গড়_ সংক্রমিত_0)/5; line_y = [average_infected_0, (slope*50)+average_infected_0]; line_x = [0, 50]; চিত্র (2) চক্রান্ত (graph_mat_x, graph_mat_y); লাইন (line_x, line_y, 'Color', 'red', 'LineStyle', '-'); শিরোনাম (['Unvaccination for Trend', disease]); xlabel ('প্রারম্ভিক অসম্পূর্ণতার শতাংশ'); ylabel ('চূড়ান্ত সংক্রমণের শতাংশ')
কোড ব্যাখ্যা
লাইন 1: সংক্রমিত শতকরা গড়ের জন্য y মান নির্ধারণ করা হয়েছে
লাইন 2: নির্ধারিত x মান প্রাথমিক শতকরা শতাংশের জন্য নির্ধারিত
লাইন 3: 0% এবং 5% এর calculateাল গণনা করুন
লাইন 4: লাইনের মান y সংরক্ষণ করুন। এটি 0% থেকে 5% বিভাগের ধারাবাহিকতা।
লাইন 5: লাইনের মান y সংরক্ষণ করুন। এই লাইনটি গ্রাফের দৈর্ঘ্য বিস্তৃত।
লাইন 6: চিত্র তৈরি করুন
লাইন 7: সংক্রমিত শতাংশের গ্রাফ x এবং y মানগুলি চক্রান্ত করুন, যারা অপ্রচলিত।
লাইন 8: লাইনটি প্লট করুন। এটি দেখানোর জন্য ব্যবহার করা হয় যে এটি রৈখিকভাবে বৃদ্ধি পায় না, বরং দ্রুতগতিতে।
লাইন 9: গ্রাফের জন্য শিরোনাম সেট করুন।
লাইন 10-11: গ্রাফের জন্য x এবং y লেবেল সেট করুন।
এখন আপনি দেখতে পাবেন যে জনসংখ্যার বৃহত্তর শতাংশ টিকা ছাড়ানো, সংক্রমণের পরিমাণ বেশি। আপনি এটাও দেখতে পাবেন যে, লাল হয়ে যাওয়া বেশিরভাগ বিন্দু সবুজ বিন্দু, যা দেখায় যে টিকা কিছু মাত্রায় সাহায্য করে! আশা করি আপনি এই টিউটোরিয়ালটি পছন্দ করেছেন। আপনার কোন প্রশ্ন থাকলে মন্তব্য করুন!
ধাপ 15: চূড়ান্ত পণ্য: সিমুলেশন কেমন দেখাচ্ছে


সমস্ত কোড এখানে পাওয়া যাবে
প্রস্তাবিত:
হার্ড ড্রাইভ: রোগ নির্ণয়, সমস্যা সমাধান এবং রক্ষণাবেক্ষণ: Ste টি ধাপ

হার্ড ড্রাইভ: রোগ নির্ণয়, সমস্যা সমাধান এবং রক্ষণাবেক্ষণ: হার্ড ড্রাইভ কি? এটিতে রয়েছে হার্ড ডিস্ক, যেখানে আপনার সমস্ত ফাইল এবং ফোল্ডার শারীরিকভাবে অবস্থিত। তথ্যটি চুম্বকীয়ভাবে ডিস্কে সংরক্ষণ করা হয়, তাই এটি ড্রাইভে থাকে এমনকি যখন
একটি ওয়্যারলেস সংস্করণ আমার গ্যারেজের দরজা খোলা নাকি বন্ধ ?: 7 টি ধাপ

একটি ওয়্যারলেস সংস্করণ … আমার গ্যারেজের দরজা খোলা নাকি বন্ধ? প্রচুর আছে " আমার গ্যারেজের দরজা খোলা আছে " প্রকল্প এই প্রকল্পগুলির অধিকাংশই হার্ড ওয়্যার্ড। আমার ক্ষেত্রে চলছে
MATLAB এর মাধ্যমে ডায়াবেটিক রেটিনোপ্যাথির স্বয়ংক্রিয় রোগ নির্ণয়: 33 টি ধাপ
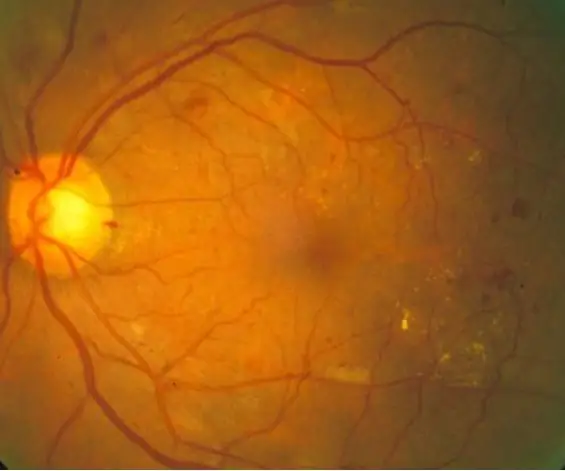
ডায়াবেটিক রেটিনোপ্যাথি ভায়া ম্যাটল্যাব এর স্বয়ংক্রিয় নির্ণয়: (উপরের কোডের রূপরেখা দেখুন) ডায়াবেটিক রেটিনোপ্যাথি একটি ডায়াবেটিস-সম্পর্কিত চোখের রোগ যা উচ্চ রক্তে শর্করার মাত্রা দ্বারা সৃষ্ট। উচ্চ রক্তে শর্করার মাত্রা রেটিনাসে রক্তনালীগুলি ফুলে যায়, যা রক্তনালীগুলিকে বড় করে তোলে এবং এমনকি জাহাজের
একটি বহিরাগত অ্যান্টেনা নিতে একটি রিকোচেট রেডিও মডেম মোড করুন: 8 টি ধাপ

একটি বহিরাগত অ্যান্টেনা নেওয়ার জন্য রিকোচেট রেডিও মডেম মোড করুন: আগের সময়ের ব্যবসায়িক মডেলের পণ্য, রিকোচেট মডেমগুলি একটি বিস্ময়করভাবে কম দামের ট্যাগ সহ দুর্দান্ত প্রযুক্তি। তারা নিয়মিত মডেমের মতো কাজ করে, কিন্তু একটি ফোন লাইনের পরিবর্তে আরএফ স্তর দিয়ে। আপনার নিজস্ব ডায়াল-ইন অ্যাক্সেস সার্ভার তৈরি করুন, একটি নিয়ন্ত্রণ করুন
পুরানো এক্সবক্স 360 হার্ড ড্রাইভ + হার্ড ড্রাইভ ট্রান্সফার কিট = পোর্টেবল ইউএসবি হার্ড ড্রাইভ !: 4 টি ধাপ

ওল্ড এক্সবক্স 360 হার্ড ড্রাইভ + হার্ড ড্রাইভ ট্রান্সফার কিট = পোর্টেবল ইউএসবি হার্ড ড্রাইভ! আর ব্যবহার করুন, সেইসাথে একটি অকেজো তারের। আপনি এটি বিক্রি করতে পারেন বা এটি দিতে পারেন … অথবা এটি ভাল ব্যবহার করতে পারেন
